
Sound Wave Propagation in a Valley (Part 2): Further Insights
Listen to article:
Understanding the concepts introduced in Part 1 of this article Sound Wave Propragation in a Valley is crucial for grasping the more detailed analysis in Part 2. Part 1 has laid the groundwork for understanding the problem of sound wave propagation in a valley, and Part 2 will build upon these concepts.
Thus, let us proceed in medias res and, drawing on the null approximation, move on to the first approximation to the problem’s interpretation.
First Approximation to the Problem’s Interpretation
All influences participating in the propagation of a warning signal remain excluded except for the geomorphology of the terrain. In the first approximation, the acoustic properties of the valley slopes are still not taken into account. The assumptions are that
- the valley is rocky without steep disproportions in the horizontal and vertical profile, and
- although the valley has perpendicular walls, it forms bends and meanders.
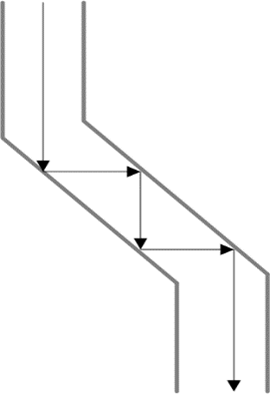
The situation is illustrated in Figure 8. The canyon effect can still be counted on, assuming that the wavefront is perpendicular to the slope of the bottom of the valley. That is, theoretically, much better than in open terrain (the reference condition) since the sound energy is still focused in the desired direction. However, the distance from the source increases due to the bends and, as commonly known, the intensity of the acoustic energy decreases with the square of the distance from the source.
Again, the sound wave vector must remain parallel to the valley’s slope.
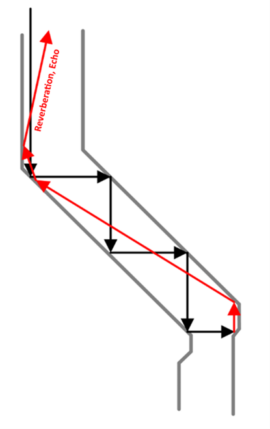
Reverberations and Echoes
In this simplified case, the sharp bends of the valley create the conditions for echoes and reverberations due to multiple internal reflections. Simply put, when a sound wave hits the bends, it bounces back and forth, creating echoes and reverberations. Reverberation means a loss of acoustic pressure in the target area because the sound wave‘s energy returns to the source and no longer propagates along the valley. Reverberations and echoes reduce the clarity of the reproduced message, as illustrated in Figures 9 and 10.

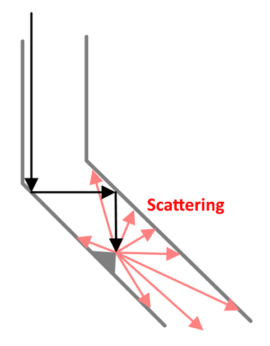
Sound Wave Scattering
The valley’s overly rugged horizontal profile creates discrete barriers to the sound wave advancing down the valley. The consequence is that the sound wave‘s energy is dissipated in all possible directions and thus lost, and the intelligibility of the acoustically propagated message is reduced. This is illustrated in Figures 11 and 12.

Second Approximation to the Problem’s Interpretation
Now that we have discussed the canyon effect, we will return to the null approximation, assuming that
- the valley is rocky and
- the valley is straight with perpendicular walls, but
- the valley’s walls are sloped; that is, they do not form a right angle with the valley bottom but are inclined to some extent.
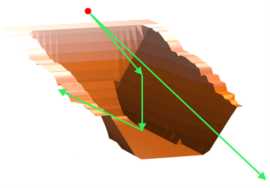
The situation is illustrated in Figure 13.
The siren is installed on the dam wall. With the sloped valley, it can be assumed that the acoustic wavefront travels unhindered along the bottom of the valley, but what happens on the side walls?
Let us apply the vector interpretation again. The sound wave vector hits the side slope of the valley at a certain angle. The vector of the advancing sound wave is reflected at the same angle and strikes the opposite slope. The angle of incidence is equal to the angle of reflection. The vector of the sound wave gradually approaches the horizontal bottom of the valley.
There is a moment when the imaginary propagation vector hits the valley bottom. Here, the situation changes because the vector of the reflected wave is orientated upwards from the plane of the valley bottom and is redirected onto the opposite slope at the same angle, where it is reflected upwards at the angle equal to the angle of incidence. The angle of the advancing wave vector doubles as a result. Depending on the steepness of the valley side walls, this may be repeated several times until the advancing wave vector leaves the valley bottom and goes up into an open space outside the target area.
The fatal conclusion is that the canyon effect quickly fades away as the multiple reflections on the side walls of the valley direct the wave upwards into an open space. In acoustics, the canyon effect is more associated with built-up urban environments (long streets lined with tall buildings).
The second approximation to the interpretation of this problem suggests that acoustic energy does not generally gather nor is directed into the valley. Hence, the designer cannot rely on the valley geomorphology’s contribution to the range of a warning signal.
The amount of information that a person can take in and process in a short time is limited. That is why the second part of the article will end just at this point. The last third part, which we will come up with shortly, will explain further approximations to the interpretation of possible propagation of a sound wave in a valley and conclude the issue.

The article was written by
Stanislav Gašpar
Stanislav worked in electronics design for a long time before transitioning to acoustics, bringing a nonconformist approach to addressing related topics. Recently, in the context of acoustics, he finds it stimulating to engage with AI, aiming to make it contradict itself and impose his own interpretation of the presented problem. Through years of experience in the technocratic industry, he has come to embrace two guiding principles: reality is orders of magnitude more complex than we interpret it, and the real fun begins when “something doesn’t work.” Additionally, he enjoys expressing his thoughts on poetry and music.
